查找非自相交闭合多边形的质心
2022-09-20 乐帮网
数学
这一节是查找非自交多边形的质心,给定多边形的 N 个顶点,任务是找到多边形的质心
例子:
Input: ar = {{0, 0}, {0, 8}, {8, 8}, {8, 0}}
Output: {Cx, Cy} = {4, 4}
Input: ar = {{1, 2}, {3, -4}, {6, -7}}
Output: {Cx, Cy} = {3.33, -3}
方法:
由 n 个顶点 (x0, y0), (x1, y1), ..., (xn-1, yn-1) 定义的非自相交闭合多边形的质心是点 (Cx, Cy),其中:
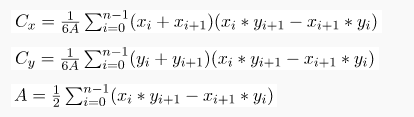
下面是上述方法的实现:
C++
// C++ program to implement the
// above approach
#include <bits/stdc++.h>
using namespace std;
pair<double, double> find_Centroid(vector<pair<double, double> >& v)
{
pair<double, double> ans = { 0, 0 };
int n = v.size();
double signedArea = 0;
// For all vertices
for (int i = 0; i < v.size(); i++) {
double x0 = v[i].first, y0 = v[i].second;
double x1 = v[(i + 1) % n].first, y1 =
v[(i + 1) % n].second;
// Calculate value of A
// using shoelace formula
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
// Calculating coordinates of
// centroid of polygon
ans.first += (x0 + x1) * A;
ans.second += (y0 + y1) * A;
}
signedArea *= 0.5;
ans.first = (ans.first) / (6 * signedArea);
ans.second = (ans.second) / (6 * signedArea);
return ans;
}
// Driver code
int main()
{
// Coordinate of the vertices
vector<pair<double, double> > vp = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
pair<double, double> ans = find_Centroid(vp);
cout << setprecision(12) << ans.first << " "
<< ans.second << '\n';
return 0;
}
Java
// Java implementation of the approach
class GFG
{
static double[] find_Centroid(double v[][])
{
double []ans = new double[2];
int n = v.length;
double signedArea = 0;
// For all vertices
for (int i = 0; i < n; i++)
{
double x0 = v[i][0], y0 = v[i][1];
double x1 = v[(i + 1) % n][0], y1 = v[(i + 1) % n][1];
// Calculate value of A
// using shoelace formula
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
// Calculating coordinates of
// centroid of polygon
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
// Driver code
public static void main (String[] args)
{
// Coordinate of the vertices
double vp[][] = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
double []ans = find_Centroid(vp);
System.out.println(ans[0] + " " + ans[1]);
}
}
// This code is contributed by AnkitRai01
Python3
# Python3 program to implement the
# above approach
def find_Centroid(v):
ans = [0, 0]
n = len(v)
signedArea = 0
# For all vertices
for i in range(len(v)):
x0 = v[i][0]
y0 = v[i][1]
x1 = v[(i + 1) % n][0]
y1 =v[(i + 1) % n][1]
# Calculate value of A
# using shoelace formula
A = (x0 * y1) - (x1 * y0)
signedArea += A
# Calculating coordinates of
# centroid of polygon
ans[0] += (x0 + x1) * A
ans[1] += (y0 + y1) * A
signedArea *= 0.5
ans[0] = (ans[0]) / (6 * signedArea)
ans[1] = (ans[1]) / (6 * signedArea)
return ans
# Driver code
# Coordinate of the vertices
vp = [ [ 1, 2 ],
[ 3, -4 ],
[ 6, -7 ] ]
ans = find_Centroid(vp)
print(round(ans[0], 12), ans[1])
# This code is contributed by Mohit Kumar
C#:
// C# implementation of the approach
using System;
class GFG
{
static double[] find_Centroid(double [,]v)
{
double []ans = new double[2];
int n = v.GetLength(0);
double signedArea = 0;
// For all vertices
for (int i = 0; i < n; i++)
{
double x0 = v[i, 0], y0 = v[i, 1];
double x1 = v[(i + 1) % n, 0],
y1 = v[(i + 1) % n, 1];
// Calculate value of A
// using shoelace formula
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
// Calculating coordinates of
// centroid of polygon
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
// Driver code
public static void Main (String[] args)
{
// Coordinate of the vertices
double [,]vp = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
double []ans = find_Centroid(vp);
Console.WriteLine(ans[0] + " " + ans[1]);
}
}
// This code is contributed by PrinciRaj1992
JavaScript:
<script>
// Javascript implementation of the approach
function find_Centroid(v)
{
let ans = new Array(2);
ans.fill(0);
let n = v.length;
let signedArea = 0;
// For all vertices
for (let i = 0; i < n; i++)
{
let x0 = v[i][0], y0 = v[i][1];
let x1 = v[(i + 1) % n][0], y1 = v[(i + 1) % n][1];
// Calculate value of A
// using shoelace formula
let A = (x0 * y1) - (x1 * y0);
signedArea += A;
// Calculating coordinates of
// centroid of polygon
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
// Coordinate of the vertices
let vp = [ [ 1, 2 ],
[ 3, -4 ],
[ 6, -7 ] ];
let ans = find_Centroid(vp);
document.write(ans[0].toFixed(11) + " " + ans[1]);
// This code is contributed by divyeshrabadiya07.
</script>
输出:
3.33333333333 -3
时间复杂度:O(n)
空间复杂度:O(1)
https://www.geeksforgeeks.org/find-the-centroid-of-a-non-self-intersecting-closed-polygon/

关注我的微信公众号
在公众号里留言交流
投稿邮箱:1052839972@qq.com
庭院深深深几许?杨柳堆烟,帘幕无重数。
玉勒雕鞍游冶处,楼高不见章台路。
雨横风狂三月暮。门掩黄昏,无计留春住。
泪眼问花花不语,乱红飞过秋千去。

如果感觉对您有帮助
欢迎向作者提供捐赠
这将是创作的最大动力
- 检查四个线段是否形成一个矩形
- 关于多边形Bentley-Ottmann算法
- 关于多边形我有想说的
- 是否有一种简单快捷的方法来检查多边形是否自相交?
- 如何判断两个线段是否相交呢?
- 李老师到某店购买计算器一个,圆规三个,三角板四块,量角器五个总付费78元
- 全球癌症的发病率20世纪下半叶比上半叶增长了近10倍,成为威胁人类生命的第一杀手。这说明
- 关闭这个核电站是反核的胜利,它同时也体现了核工业很迟才肯承认它们不能安全运作这样的发电站的事实
- 赵明、钱红、孙杰三人被北京大学、清华大学和北京师范大学录取。他们分别被哪个学校录取的
- 甲乙清晨锻炼,甲步行锻炼30分钟,乙跑步锻炼,跑步的速度是甲步行速度的5倍,跑步路程是甲步行路程的3倍,乙跑步锻炼___分钟